Chess Knight Possible Moves Algorithm with Drawing

At first, I will define and explain the algorithm and its solution with a drawing. At the end of the post, I will show you how I solve the algorithm in Java.

Problem

Our algorithm will progress on a classic 8x8 chessboard that is empty. We will give the algorithm the abscissa and ordinate of the position where we put the knight, and the algorithm will try to find out how many different points the knight can move in this position.

Solution

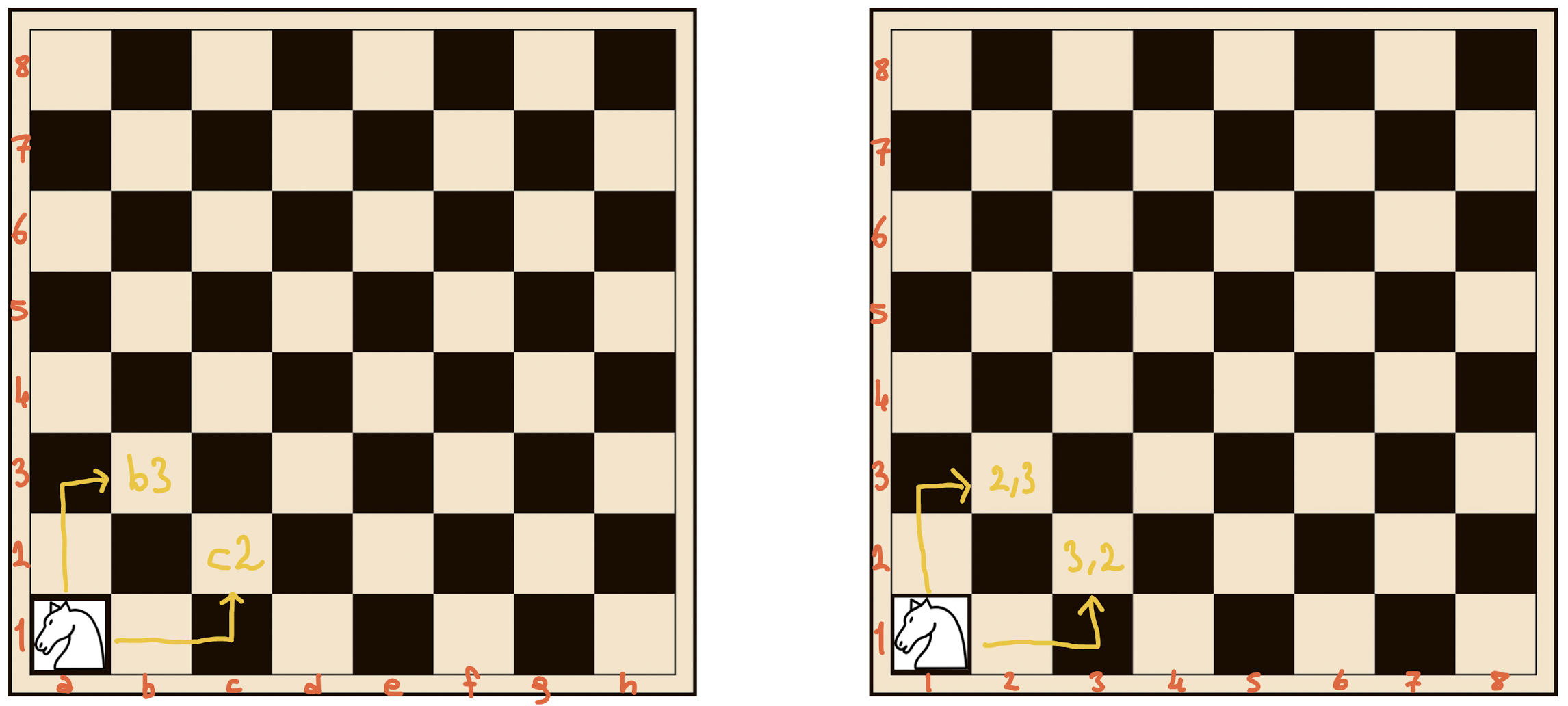
The chess coordinates are like the picture on the left; b3, c2, and so on. But when solving the knight jump algorithm, we will think like the picture on the right. The abscissa and ordinate will be numeric values such as (1, 1) or (2, 3).

Why do we think this way? Let's explain with a Coordinate System.

Let's place this Coordinate System on the knight, like below. But for easier understanding, let's first place it in the area where the knight can move the most move on the chessboard.

Now, you can see the knight can 8 different moves. Also, you can see that all of the knight moves stayed in the Coordinate System between -2 and +2. Now, just through simple math operations, we can change the knight's position.

Let's see how the knight can move to the 1 (2,6) position.

• The knight X coordinate (on the chessboard): 4
• 4 - 2 = 2 is on the chessboard? Yes, it's between 1 and 8.
• The knight Y coordinate (on the chessboard): 5
• 5 + 1 = 6 is on the chessboard? Yes, it's between 1 and 8.
• Then we can say that the last position (2,6) is our 1 position.

If you are aware, all moves step by step [-2, +1] --> 1. position. [-2, -1] --> 2. position and so on... Always. 

So, what if the knight is on the edge of the chessboard? Let's see.

Let's see how the knight can move to the 1 (-1, 2) position again.

• The knight X coordinate (on the chessboard): 1
• 1 - 2 = -1 is on the chessboard? No, it's not between 1 and 8.
• The knight Y coordinate (on the chessboard): 1
• 1 + 1 = 2 is on the chessboard? Yes, it's between 1 and 8.
• Then we can say that the last position (-1,2) is our 1 position, and it's not on the chessboard because abscissa or ordinate cannot be a negative value.

Yes, that's it. Now, we know which positions are on the chessboard and which are not, right?

Here it's my solution in Java.

public class KnightJumpsApp {
    public static int knightJumps(String str) {
        int counterCanMovePositions = 0;
        int x = str.charAt(1) - '0'; // i.e: The knight x coordinate (on the chessboard): 1
        int y = str.charAt(3) - '0'; // i.e: y : 1
        int newX, newY;
        
        int[][] allPotentialPositions = {{-2, 1}, {-2, -1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};

        for (int i = 0; i < allPotentialPositions.length; i++) { // Let's try all the potential positions...
            newX = x + allPotentialPositions[i][0]; // i.e: newX = 1 + (-2) = -1
            newY = y + allPotentialPositions[i][1]; // i.e: newY = 1 + 1 = 2
            if (newX > 0 && newX < 9 && newY > 0 && newY < 9) { // if newX and newY positions between 1 and 8
                System.out.println("(" + newX + " " + newY + ")"); // show new coordinate
                counterCanMovePositions++;
            }
        }

        return counterCanMovePositions;
    }

    public static void main(String[] args) {
    	// Tests
        System.out.println("1) 2 = " + knightJumps("(1 1)"));
        System.out.println("2) 8 = " + knightJumps("(5 5)"));
        System.out.println("3) 3 = " + knightJumps("(2 8)"));
    }
}